[밑바닥 부터 시작하는 딥러닝] 2장~5장- 주요 용어 정리

* 퍼셉트론 : 

인공뉴런, 신경망(딥러닝)의 기원이 되는 알고리즘

 

 

* 활성화함수 : 
입력신호의 '총 합'을 출력신호(1,0)으로 변환하는 함수 

(예측한 다중회귀 식을 출력값(y)인 0과 1로 변환해 주기 위한 함수)

- 시그모이드, 계단, 렬루 함수 등이 있음.

 

* 노드 : 뉴런을 의미. (신경망 그림에서의 원을 의미)

 

* [출력층 설계하기]

- 신경망은 분류와 회귀 모두에 이용할 수 있으나, 출력층에서 사용하는 활성화함수는 둘 중 어떤 문제냐에 따라서 달라진다. 

* 기계학습 문제에는 분류와 회귀가 있다. 분류는 말그대로 데이터가 어떤 클래스에 속하는지를 예측하는 문제강아지냐 고양이냐), 회귀는 입력데이터에서 (연속적인) 수치를 예측하는 문제(사진속 인물의 키(163.7?)를 예측)이다. 말그대로 회귀분석.

-> 일반적으로 회귀문제에는 항등함수를 

                   분류문제에는 소프트맥스 함수를 사용함. 

 

* 항등함수 : 입력을 그대로 출력하는 함수. 말그대로 입력과 출력이 항상 같다(항등하다)는 의미. 

* 소프트맥수 함수 : 

함수식 표현은

소프트맥스를 사용하는 분류문제에서 이렇게 출력값이 출력됨. 

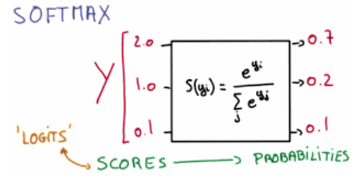
-소프트맥스 함수를 거친 값들은 0과 1사이의 값을 가지는 확률로 생각할 수 있다.

-- 궁금한 것. 머신러닝과 딥러닝에서의 분류와 회귀, 딥러닝에서는 주로 이미지처리나 자연어처리인 것으로 아는데 회귀 문제가 있나? 머신러닝에서는 분류도 회귀도 가능?

 

 

* 선형함수 :

출력이 입력의 상수배만큼 변하는 함수

 

* 원 핫 인코딩 : 

정답을 뜻하는 원소만 1이고 나머지는 모두 0인 배열로 만드는 방법.

 

 

 

[ 4장. 신경망 학습 ]

 

* 학습 :

훈련데이터로부터 가중치 매겨변수(w)의 최적값을 찾는것. 

 

• 손실함수 : 

- 신경망이 학습할 수 있도록 해주는 지표가 되는 것이 손실함수. 

- 손실함수의 결과값을 가장 작게 만드는 가중치를 찾는 것이 학습의 목표. 

- 손실함수의 값을 작게 만드는 기법으로, 함수의 기울기를 활용하는 경사법(경사하강법)을 4장에서 소개. 

 

학습률에 따라 손실함수가 어떻게 달라지는지

 

- 손실함수는 신경망 성능의 나쁨을 나타내는 지표이다. 즉 클수록 나쁘고 작을수록 좋은 것. 

 

- 일반적으로 많이 쓰이는 손실함수는 평균제곱오차(MSE)와 교차 엔트로피 오차(cross entropy error, CEE)가 있다. 

 

* 1) 평균 제곱 오차(MSE) : 

- 가장 많이 쓰이는 손실함수

함수 식으로 표현하면 

Y는 신경망의 출력(신경망이 예측한 값), t는 정답 레이블, k는 데이터의 차원수를 의미. 

일반적으로 수리통계학에서 이렇게 표현하는 함수이다.  (f(x)만 바꾼거)

- 평균 제곱 오차 MSE는 위 식에서 알 수 있듯이 각 원소의 추정값에서 참값을 뺀 오차(y-t)의 제곱의 총합을 구한다.

--->? . 수리통계학에서는 오차의 제곱의 평균을 구하기 위해 말그대로 제곱해서 n으로 나눠주는데 여기서는 왜 2로 나누지? 그리고 2로 나눠서 평균이 되는 것도 아닌데 왜 평균제곱오차라고 하지? 이건 말그대로 제곱오차의 평균이라는 의미 아닌가..

 

* 2) 교차 엔트로피 오차 

y는 신경망의 출력, t는 정답 레이블,

tk는 정답에 해당하는 인덱스의 원소만 1이고 나머지는0임(원핫인코딩).

그래서 위 식은 정답의 추정값(tk가 1일때의 yk)의 자연로그를 계산하는 식이 됨. 

- 즉 교차엔트로피오차는 정답일 떄의 출력이 전체 값을 정하게 됨.

---> ? 이거 정답이 아닐때는 t가 0이 되니까 정답인 값 빼고는 다 0 되서 지워진다는 의미인가? 그러면 더하는게 무슨 의미가 있지?

 

그렇다면 손실함수의 최소값을 구하려면 어떻게 해야할까? 

* 경사하강법 : 손실함수의 최소값을 구하기 위한 방법으로 함수의 기울기가 0이되는 지점이 바로 함수의 최소값이 되므로(아래로 볼록 함수의 최소값은 기울기가 0이므로) 이 지점을 찾는 방법을 경사하강법이라고 함. (경사 상승법은 최대값을 찾는 것. 통추에서 배운 MLE. 여기에 -마이너스만 붙여도 경사하강법이 됨. )

 

[ 5장. 오차역전파법 ]

: 오차를 역 방향으로 전파하는 방법(=역전파,역전파법)

 

* 에지edge : 노드 사이의 직선

 

* 순전파 : 왼쪽에서 ---> 오른쪽으로 진행하는 단계를 순전파라고 함. 

- 이것의 반대방향으로 전파하는 것을 역전파라 함. 

 

• 역전파

- 미분계산을 할 때 중요하게 쓰임.

역전파를 도식으로 표현하면 아래와 같이 순전파를 통해 나온 오차를 가지고 역전파를 시켜서 가중치를 업데이트 시키는 것. 

역전파에 대한 내용은 이해가 잘 가지 않아서 아래의 블로그들을 참고하였다. 

https://m.blog.naver.com/samsjang/221033626685

 

 

[35편] 딥러닝의 핵심 개념 - 역전파(backpropagation) 이해하기1

 

https://ratsgo.github.io/deep%20learning/2017/05/14/backprop/

오차 역전파 (backpropagation) · ratsgo's blog

역전파에 대한 내용중에 미분을 왜 저렇게 편미분을 해서 하는 건지에 대한 내용이 잘 이해가 가질 않는다.