728x90
줌 세션
- 지도학습이 뭘까?-정답을 주고 예측을 학습시키는 것
- -답이 있는 데이터 (라벨이든 목적변수든)
- 비지도학습과 지도학습 비교-가장 중요한건 내가 이 데이터로 뭘 할건지의 목표를 설정하는 것.
- -군집화를 할 것 인지 예측을 할 것 인지.
- 기준모델이란?
- 회귀 문제의 경우 데이터의 평균값을 기준값으로 한다.
- 이후 내가 만든 머신러닝 모델의 성능이 어느정도 되는지 알아보려고
- 기준모델과의 평균제곱오차와 비교한다.
warm-up
- 일단 유툽에서 영어로 한번 쭉 보기.
- 단어별로 먼저 보고
- 문장별로 읽으면서 보자.
Lecture에서 배운 것
- 회귀모델에서 지표중 하나인 MAE(절대평균오차)는 계산을 해도 실제 목적변수의 단위와 달라지지 않아서 비교를 할 때 유용하다!

도전과제
6) 단선선형회귀는 선형성, 정규성, 등분산성 등의 가정이 성립해야 한다.
- 선형성 : 산점도를 찍어 보았을 때, 마구잡이로 흩뿌려진 것이 아니라 어느정도 상관관계를 보이는지.
- 정규성 : 잔차의 분포가 정규분포를 따르는지. (잔차의 히스토그램으로 확인 or Shapiro-Wilk Test)
- 등분산성 : 잔차만을 가지고 보았을 때 잔차가 특정한 패턴 없이 고르게 분포하고 있는지. (잔차의 산점도로 확인)
- 잔차의 기대값은 0
이러한 기본 가정을 만족해야 유의한 회귀모델을 만들 수 있음.
7) OLS최소제곱법인 OLS는 잔차의 제곱합이 최소가 되계 하는 회귀식의 모수 을 찾는 방법이다.
실제값과 회귀선을 통해 예측한 예측값의 차이를 잔차라고 하고, 이 잔차들을 가장 작게하는 회귀선이 가장 좋은 회귀선이라고 할 수 있다.그렇다면 이 회귀선을 찾으려면 어떻게 해야할까? 우선 이러한 잔차에 대한 지표로는 잔차를 제곱하는 방법, 잔차에 절대값을 씌워 더하는 방법 등이 있는데 잔차에 절대값을 씌워 더하는 방식은 식이 복잡해졌을 때 미분이 되지 않으므로 최솟값을 갖게하는 모수를 찾기에 유용하지 않다. 따라서, 제곱이 되어 미분이 가능한 잔차제곱합을 지표로 하여 이를 최솟값을 만들어주는 모수(회귀계수)를 찾는다. ( 최솟값이 되는 지점은 잔차제곱합의 식의 미분값 즉, 기울기가 0이되는 지점을 찾으면 된다)
직선 방정식이f(x)=ax+b이라면, 각 점xi의 좌표값yi와 함수값f(xi)의 오차yi-f(xi) = yi-(axi+b)의 제곱의 합이 최소가 되는 경우이다. 즉, 다음 식이 최소가 되는 경우이다.
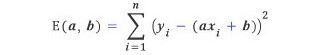
이러한 식을 최적의 최소 제곱직선이라고 부르는데, E(a, b)의 최솟값은 a와 b에 의해 결정되므로 직선의 기울기 a와 절편 b의 값을 찾는 것이 열쇠가 된다. 어떻게 a, b를 찾을 수 있을까? E(a,b)가 최소값이 되려면 미적분학의 이론에 의해 편미분 ∂E/∂a와 ∂E/∂b가 0이 되어야 한다. 즉, 다음과 같다.
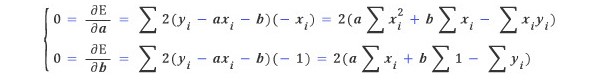
→ 이 오차항을 a와 b에 대해서 편미분한 식을 0으로 두고 풀었을 때 나온 두 연립방적식을 통해 a와 b를 이렇게 구할 수 있다.

728x90
'코드스테이츠 Ai Boostcamp' 카테고리의 다른 글
| [Tree Based Model]Decision Trees(의사결정나무) (0) | 2021.06.15 |
|---|---|
| [선형모델]Multiple Regression(다중선형회귀) (0) | 2021.06.12 |
| [n13x] Sprint Challenge (0) | 2021.06.12 |
| [선형대수] 클러스터링(군집분류) (0) | 2021.06.12 |
| [선형대수]Dimension Reduction(차원축소) (0) | 2021.06.12 |



댓글