머신러닝 지도학습에서 쓰이는 회귀분석 모델
머신러닝의 지도학습에서 쓰이는 통계학의 회귀분석 4가지 모델에 대해서 알아보자.
(이는 공부한 것을 정리하기 위한 포스팅으로 틀린 부분이 있을 수 있습니다.)
단순선형회귀
하나의 독립변수로 종속변수를 예측할 때 쓰이는가장 기본적인 회귀분석 방법이다.
독립변수와 종속변수간의 상관관계가 어느정도 있을 때 시도할 수 있다.
공식
$$\hat{Y} = aX + b$$
단순선형 회귀식의 모수는 예측값에서 실제값을 뺀 오차를 최소화하는 값으로
이를 구하는 공식은 아래와 같다.
$$a = \frac{S_{xy}}{S_{xx}}, b = \bar{y} - a\bar{x}$$
다중선형회귀
다중선형회귀는 단순선형 회귀에서 독립변수의 수가 2개 이상으로 늘어난 것으로
똑같이 오차를 최소화하는 방식의 최소제곱법으로 회귀계수를 구한다.
최소제곱법은 OLS라고도 부른다.
공식
$$\hat{Y} = a_1X_1 + a_2X_2 + ... + a_iX_i + b $$
이를 행렬식으로 표현하면 아래와 같다.
$$\hat{Y}
= AX + b$$
릿지회귀
릿지회귀는 능형회귀라고도 부르며, 다중선형회귀의 과적합을 해결하기 위한 방법이다. 이를 위해 최소제곱법 과정에 가중치를 두며 이는 상수항에 곱해진 람다이다.
릿지회귀의 공식은 아래와 같다.
$\beta_{ridge}$: $argmin[\sum_{i=1}^n(y_i - \beta_0 - \beta_1x_{i1}-\dotsc-\beta_px_{ip})^2 + \lambda\sum_{j=1}^p\beta_j^2]$
(n: 샘플수, p: 특성수, λ : 튜닝 파라미터(패널티))
여기서 람다가 0이면 다중회귀분석 모델이 된다. 이 람다 값을 적절하게 설정하여 과적합을 방지하면서도 테스트셋에도 일반화가 잘 되게 하는 것이 릿지회귀의 목적이다. 이러한 모델을 정규화모델이라고 한다.
정규화의 강도를 조절해주는 패널티값인 람다는 다음과 같은 성질이 있다.
λ → 0, $\beta_{ridge}$ → βOLS
λ → ∞, $\beta_{ridge}$ → 0.
릿지회귀 사이킷런 함수 코드
from sklearn.linear_model import Ridge
model = Ridge(alpha=alpha, normalize=True)
model.fit(X_train, y_train)로지스틱 회귀
로지스틱 분석은 회귀분석에서 0과 1/ 사망 또는 생존과 같이 이진분류된 종속변수를 에측하기 위한 회귀분석 방법으로, 1에 속할 확률 또는 생존에 속할 확률을 0과 1사이의 확률값으로 반환한다. (로지스틱은 0과 1사이의 연속적인 값을 반환하므로 이름에 회귀가 들어가긴 하지만 주로 머신러닝에서 분류문제에 쓰이므로 지도학습에서 분류 카테고리에 있다고 보면 된다.)
공식
- 오즈
$Odds = \large \frac{p}{1-p}$,
p = 성공확률, 1-p = 실패확률
오즈는 성공확률에 대한 실패확률의 비로 성공확률이 1에 가까워질 수록 오즈는 무한대에 가까워지고, 성공확률이 0으로 작아질 수록 오즈도 0이 된다.
- 로짓변환
오즈에 로그를 취한 함수로, 입력 값의 범위가 [0,1] 일때 출력 값의 범위를 ${\displaystyle (-\infty ,+\infty )}$로 조정한다.
$\operatorname{logit}(p) = \log\frac{p}{1-p}$
- 로지스틱 함수
로지스틱 함수는 로짓 변환을 통해 만들어지고, 그 형태는 다음과 같다.
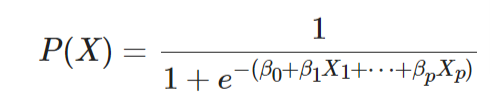
$$ 0 \leq P(X) \leq 1$$
이를 그래프로 나타내면 다음과 같다.
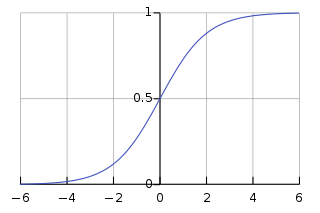
그냥 시그모이드 함수로 e의 차수에 회귀식이 들어간다고 생각하면 된다.
(시그모이드 함수는 연속적인 값을 0과 1 사이의 값으로 변환해주는 함수이다)
이렇게 0과 1 사이의 값으로 반환된 라벨에 대한 확률값으로 주로 0.5보다 크면 1 작으면 0으로 분류한다.
로지스틱 사이킷런 함수 코드
from sklearn.linear_model import LogisticRegression
logistic = LogisticRegression()
logistic.fit(X_train, y_train)
댓글